2019. 12. 3. 15:33ㆍ공부/TIL
TIL #026
191203 화
오늘 배운 점
<Flutter>
1. 3단바 Drawer 만들기
- Scaffold 안에 Drawer()를 활용하여 만들어준다. 여기서 헤더에 사용자 정보(프로필 사진, 닉네임, 아이디 등)를 출력할 수도 있다.
//Scaffold 안에
drawer: Drawer(
child: ListView(
padding: EdgeInsets.zero,
children: <Widget>[
DrawerHeader(
child: Text('Drawer Header'),
decoration: BoxDecoration(color: Color(Global.hexColor('#FB4D41'))),
),
ListTile(
title: Text('Item 1'),
onTap: () {
Navigator.pop(context);
//Navigator.of(context).push(MaterialPageRoute(builder: (BuildContext context) => NewPage("Page two")));
},
),
ListTile(
title: Text('Item 2'),
onTap: () {
Navigator.pop(context);
},
),
],
),
),
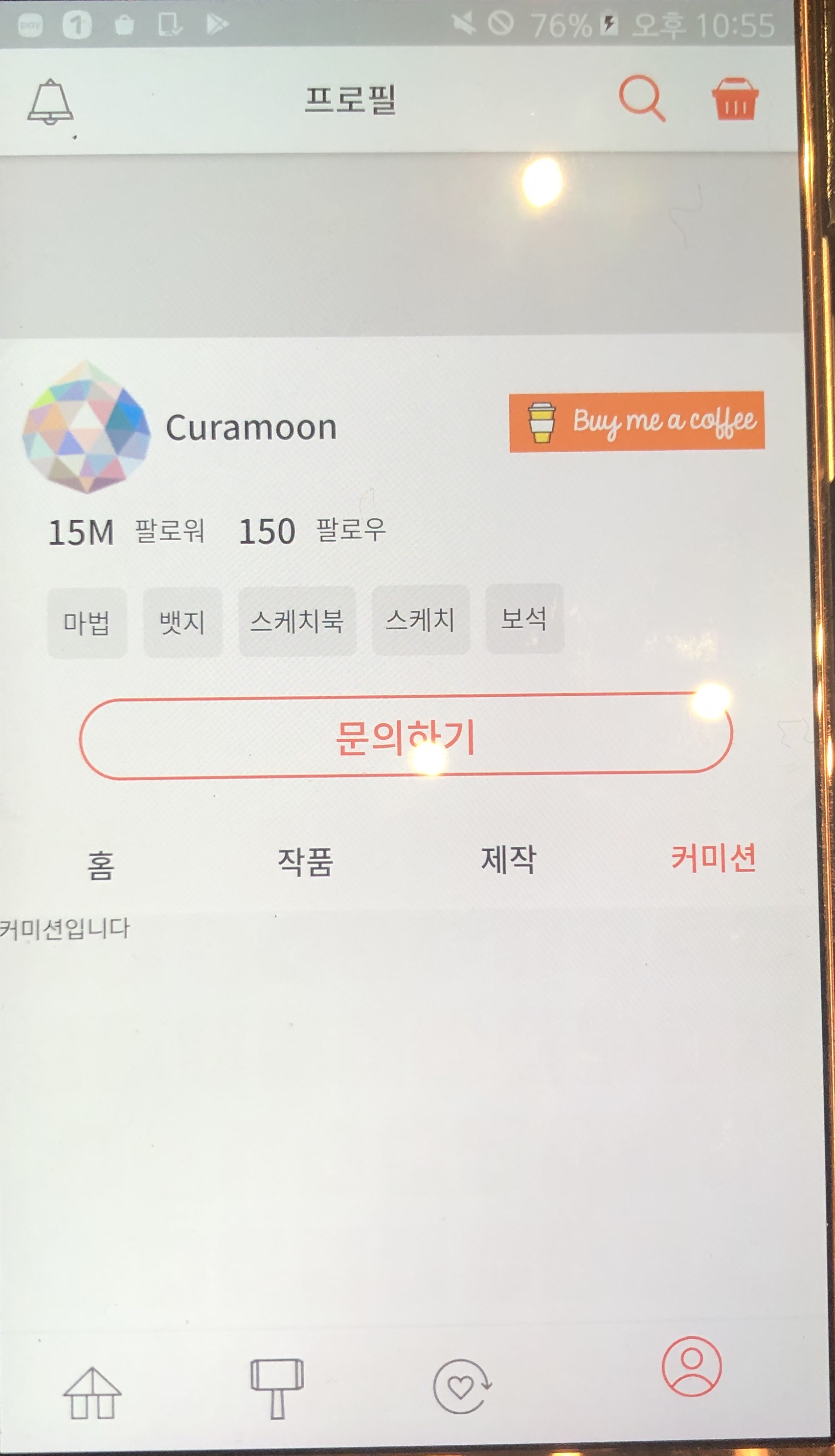
2. 마이스튜디오 화면 구현
- 결국 스토어탭에서 사용하던 DefaultTabController 안에 NestedScrollView를 body로 하고 headerSliverBuilder와 하위 body에 TabBarView를 두는 방식으로 탭 구현을 하였다. 이렇게 되면 둥근 모서리 UI 구현에서 문제가 생기는데, 어떻게 해결할지 아직 고민중이다.
<학교 전공 공부 - 경영경제자료분석>
어제 공부한 내용에 이어 시계열 자료 회귀분석을 더 공부했다. 수업에서 교수님이 가장 강조한 단원 중 하나기도 하고, 시험 비중도 커서 좀 시간을 길게 두고 공부하고 있다.
1. 시계열 회귀분석 모형의 주된 목적은 인과관계의 추정보다는 예측에 가깝다.
- 추정계수가 일치성, 불편성을 가져야 하는 것보다는 설명력이 중요하다. (결정계수 R^2, AIC, BIC 등이 활용된다)
2. 먼저 시도표를 그려보며 시각적으로 정상계열인지 비정상계열인지를 파악하고, 이분산성을 확인한다.
- 비정상성이란, 과거와 미래의 확률이 다름을 말한다. 경제시계열은 주로 로그를 취하거나 로그차를 사용한다.
3. 한 시점에서 다음 시점과 연관되는 것을 자기상관(Autocorrelation)이라 하는데, 변수가 정상이면 V(y_t) = V(v_t-j)이다.
- 자기상관함수(ACF)를 통해 데이터의 계열상관 및 자기상관을 확인할 수 있다.
- 비정상 SACF는 느리게 감소하는 반면, 정상 SACF는 빠르게 0 근처로 감소하는 특징이 있다.
- 정상성을 가진 자료는 시계열 값이 평균에서 벗어나게 되어도 다시 평균으로 돌아가려는(mean reverting) 성질을 가지고 있다.
- 강한 양(+)의 자기 상관을 가지면 장기 추세가 있음을 알 수 있으며, 이는 특정 값이 그 인근 값과 유사한 경향이 있다는 것을 말한다. 음(-)의 자기 상관은 진동패턴을 의미하는데, 이는 특정 시점의 변화량이이 양수면 그 직전/직후 시점 변화량은은 음수인 경향이 있다는 것이다.
4. 시계열 예측에서 가장 간단하게 세울 수 있는 것은 자기회귀모형(Autoregression)이다. 종속변수아 설명변수가 같은 변수이며, 오차 u_t는 무자기상관계열이다.
- 회귀계수의 부호를 통해 현 시점의 값이 다음 시점에 어떤 식으로 영향을 주는지 알 수 있다.
- 여기에서 적합치(fitted value)와 다른 개념인 예측치 및 예측오차가 등장하는데, 전자는 sample 내, 후자는 out-of-sample에 관한 것이라는 차이가 있다.
- 예측의 정확성을 검토하기 위해 RMSFE를 척도로 사용하는데, 이는 예측 오차의 표준편차의 추정치이다. 참고로 예측 오차는 미래값을 모르게 때문에(u_t) + 모수추정에 기인하는 오차로 구성되는데, n이 크면 추정오차는 점점 0에 수렴하게 된다.
- AR(1) 모형에서 예측력을 평가한 후, 예측을 개선하기 위해 더 많은 과거값을 사용하는 고차 AR 모형을 고려하거나 추가 예측변수가 있는 시계열 모형인 ADL(Autoregressive Distributed Lag) 모형을 사용하게 된다.
5. ADL 모형에서 추가된 예측변수의 예측력을 검정할 때는 Granger Causality 방법을 사용한다.
6. 시차를 결정하는 방법은 여러가지가 있는데, 모형적합도와 모형복잡도(추정의 불확실성) 간의 균형을 이루는 게 중요하다.
- F통계량으로 유의성을 검정하며 차수를 하나씩 줄여가며 검정할 수 있지만, 이 방법은 번거로우므로 보통 BIC나 AIC를 활용한다.
7. 비정상성의 추세(trend) - 확정적 추세(deterministic)와 확률적 추세(stochastic)가 있다. 대부분의 경제시계열 자료는 후자에 해당하는데, 대표적인 모형으로 random walk가 있다.
- random walk에서 내일의 최적예측치는 오늘의 값이다. 여기에 모형의 움직이는 방향(beta_0)하면 random walk with drift 모형이 된다. 둘 다 비정상성을 가지는데, 이를 증명할 때에는 u_t가 serially uncorrrelated함을 활용하여 y_t의 분산이 t에 의존한다는 것, 혹은 두 시점의 y 분산이 일치하지 않는다는 것을 활용한다.
- AR 모형의 안정조건(정상성)은 beta_1의 절댓값이 1 미만일 때다. 이는 추정된 회귀식에서 회귀계수를 활용하여 특성방정식을 세우고, 각 근이 이 조건을 충족하는지 확인함으로써 알 수 있다. 두 근의 계수 합이 1이면 근 중에 단위근 1이 존재한다는 것을 의미한다(비정상).
8. 확률적 추세의 문제점은 크게 3가지가 있다.
- 추정계수가 0을 향해 편의된다는 것
- 가설 검정에 사용하는 t 통계량은 정규분포를 따르지 않는다는 것 (그래서 기각역은 1.96, 2.58이 아닌 critical value를 따로 확인한다.)
- 그리고 허구적 회귀의 가능성이 있다는 것이다. (단위근 계열 회귀분석을 통해 도출될 수 있는 다른 결론으로는 공적분 회귀가 있다. correlation은 정상계열 자료에만 사용하므로 cointegration을 통해 비정상계열 자료에 사용한다.)
9. 단위근 계열인지 판별하는 데에는 주로 Dickey-Fuller test가 사용된다.
- 추세가 없는 자료의 대립가설은 정상계열인지에 관한 것이고, 추세가 있는 자료의 대립가설은 확정적 추세인지에 관한 것이다.
10. 확률적 추세로 인한 문제를 피하기 위해 원계열이 단위근 계열이라면 이를 차분하여 회귀분석을 수행한다. (차분하면 stationary)
내일 배울 점
<Flutter>
1. 굿즈 DB를 위한 아이템 조사 완료 및 업로드
2. 3단바 수정
3. SNS 홍보 계정 퍼미션 체크
<학교 전공>
- 경영경제자료분석 공부
- 컴퓨터네트워크 공부
-생각조각을 쓸 시간은 없다 하하
'공부 > TIL' 카테고리의 다른 글
| TIL #028 시험 뒤에 과제 뒤에 시험 (0) | 2019.12.05 |
|---|---|
| TIL #027 하루만 더 고민해보면 답이 나오기도 한다 (0) | 2019.12.04 |
| TIL #025 화면을 찍어내자 헛둘 (0) | 2019.12.02 |
| TIL #024 통계통계한 공부만 한 날 (0) | 2019.12.01 |
| TIL #023 시험기간에 코딩하기 (0) | 2019.11.30 |